
Solitude渲染数学公式Katex配置
一、前言
前两天准备写一篇关于猫脸变换的文章,里边需要穿插许多公式,Solitude主题是默认支持Katex的,打开enable配置,也在文章的Front-Matter中开启了katex配置,但是在渲染的时候,发现公式并没有按照预期的效果,经过一番折腾,找了许许多多的资料,最终还是得自己摸索出来了正确的配置方法。
数学公式的准确且美观是提升内容专业性的重要环节,而Katex是一款强大的数学公式渲染引擎,它能够将数学符号和公式转化为美观的图像,为文章增添了视觉上的冲击。
并且Solitude主题默认支持了Katex的渲染,但是仍然存在一些小问题,需要自己手动进行一些修改,才能达到预期的效果。
推荐:Katex
二、Katex与Latex简介
(一)Katex
- 简介:专为 Web 端优化的轻量级数学公式渲染引擎,基于 Latex 语法简化而来,通过纯 JavaScript 实现前端公式渲染。
- 优点:
- 轻量高效:文件体积仅约 100KB,加载速度快,不影响页面性能
- 语法兼容:支持 80% 以上基础 Latex 语法,学习成本低
- 前端直出:无需后端编译,直接在浏览器中渲染
- 移动友好:在手机、平板等设备上渲染效果一致
- 缺点:
- 复杂公式支持有限:不支持交换图、部分 AMS 宏包特性
- 宏包扩展缺失:无法使用 Latex 的宏包机制扩展功能
(二)Latex
- 简介:学术界主流的文档排版系统,以 TeX 为基础,通过宏包机制实现复杂数学公式及文档格式的精确控制,需编译后生成 PDF 等格式。
- 优点:
- 专业权威:学术出版领域黄金标准,支持超复杂公式排版
- 功能全面:通过 amsmath、amssymb 等宏包实现无限扩展
- 格式规范:自动处理公式编号、引用及文档整体排版
- 缺点:
- 性能开销大:Web 端通过 MathJax 加载时体积超 500KB,渲染延迟高
- 集成复杂:需后端编译或前端复杂配置,不适合快速集成
- 学习门槛高:语法体系复杂,需掌握文档结构与编译流程
三、对比分析
与其他工具在渲染性能、语法兼容性、集成难度、适用场景等方面进行了对比,以帮助读者更好地选择适合的工具。
| 对比维度 | Katex | Latex(通过MathJax) | 原生HTML+CSS | 后端渲染 |
|---|---|---|---|---|
| 渲染性能 | 极快(100KB,低延迟) | 较慢(500KB+,高延迟) | 最佳(仅基础公式) | 依赖网络,可能闪烁 |
| 语法兼容性 | 基础Latex语法兼容 | 完整Latex语法支持 | 无统一语法 | 完整Latex语法支持 |
| 集成难度 | 简单(引入2个文件) | 中等(需复杂配置) | 极低(手动编写) | 高(需服务器环境) |
| 适用场景 | 技术博客、移动端 | 学术论文、复杂公式 | 极简公式应急排版 | 高质量打印场景 |
四、Solitude 主题配置数学公式渲染教程
(一)主题配置修改
直接切换到Solitude主题配置文件,然后 Ctrl+F 搜索 katex ,找到 katex 配置项,设置enable为true
其余两项,根据自己的需求进行配置即可,不过推荐per_page: false,因为这样可以让Katex不用在每个页面都加载,避免Katex的加载时间过长,影响页面的加载速度。
1 | # Katex |
(二)渲染器选择
Solitude主题,推荐hexo-renderer-kramed渲染器
安装方法:
1 | npm install hexo-renderer-kramed --save |
目前有很多主流的渲染器,包括:
- hexo-render-marked
- hexo-render-kramed
- hexo-renderer-pandoc
- hexo-renderer-markdown-it
- hexo-renderer-markdown-it-plus
由于Solitude主题默认的是hexo-renderer-marked,并且经过ByteWyrm的多次测试
Solitude主题只支持:
- hexo-renderer-marked
- hexo-renderer-kramed
如果使用其他三种渲染器,会报错:Template render error: (unknown path) Error: filter not found: attr
但是由于Hexo默认的渲染引擎hexo-renderer-marked存在一些问题,并且对公式的支持不是很好,hexo-renderer-kramed是在hexo-renderer-marked的基础上进行了一些修改和优化,所以我们选择hexo-renderer-kramed作为我们的渲染器。
(三)插件安装与Front_Matter配置
1.卸载默认渲染器hexo-renderer-marked
1 | npm uninstall hexo-renderer-marked --save |
2.安装渲染器hexo-renderer-kramed
1 | npm install hexo-renderer-kramed --save |
3.安装hexo-filter-mathjax
1 | npm install hexo-filter-mathjax --save |
4.Front_Matter配置
1 |
|
5.三连更新
1 | hexo clean ## 清除缓存 |
五、更改转义规则
关键文件:
- /node_modules/kramed/lib/rules/inline.js
- /node_modules/kramed/lib/renderer.js
(一)inline.js修改:
1.第11行,解决:反斜杠\被转义为\而非LaTeX换行符的问题
问题描述:当公式中出现\表示换行时,会被kramed渲染为\,导致公式显示异常。
原:
1 | escape: /^\\([\\`*{}\[\]()#$+\-.!_>])/, |
修改为:
1 | escape: /^\\([`*\[\]()# +\-.!_>])/, |
2.第20行,解决:下划线_被转义为斜体而非LaTeX下标
问题描述:当公式中出现多个下划线时,会被kramed渲染为Markdown斜体,导致公式显示异常。
Markdown本身的语法是支持*和_都被转义为斜体的,所以我们可以取消掉kramed对_的转义。
原:
1 | em: /^\b_((?:__|[\s\S])+?)_\b|^\*((?:\*\*|[\s\S])+?)\*(?!\*)/, |
修改为:
1 | em: /^\*((?:\*\*|[\s\S])+?)\*(?!\*)/, |
3.第64行,解决:反斜杠加竖线\|被转义为|而非LaTeX双竖线
问题描述:当公式中出现\|表示紧贴符号时,会被kramed渲染为|,导致公式显示异常。
原:
1 | escape: replace(inline.escape)('])', '~|])')(), |
修改为:
1 | escape: replace(inline.escape)('])', '~])')(), |
(二)inline.js修改
修改这个文件的主要目的是为了修复:hexo-renderer-kramed不能渲染Todo List
找到第88行
原:
1 | Renderer.prototype.listitem = function(text) { |
修改为:
1 | // Support To-Do List |
六、Katex基本公式
(一)行内公式($)
行内公式是指将公式嵌入到文本中的公式,通常使用一对美元符号($)括起来,例如:
MarkDown文档:$$E=mc^2$$
渲染效果:
(二)行间公式($)
行间公式是指单独占一行的公式,通常使用一对双美元符号($$)括起来
但是注意:Solitude主题行间公式也使用($)
[❌]MarkDown文档($$):
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
$$
\begin{cases}
x' = (x + y) \mod N \\\
y' = (x + 2y) \mod N
\end{cases}
$$
其**矩阵形式**可表示为:
$$
\begin{pmatrix}
x' \\
y'
\end{pmatrix}
=
\begin{pmatrix}
1 & 1 \\
1 & 2
\end{pmatrix}
\begin{pmatrix}
x \\
y
\end{pmatrix}
\mod N
$$
**行列式分析**:变换矩阵的行列式为:
$$
\det
\begin{pmatrix}
1 & 1 \\
1 & 2
\end{pmatrix}
= 1 \times 2 - 1 \times 1 = 1
$$[❌]渲染效果:
[✅]MarkDown文档(
$):
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
$
\begin{cases}
x' = (x + y) \mod N \\\
y' = (x + 2y) \mod N
\end{cases}
$
其**矩阵形式**可表示为:
$$
\begin{pmatrix}
x' \\\
y'
\end{pmatrix}
=
\begin{pmatrix}
1 & 1 \\\
1 & 2
\end{pmatrix}
\begin{pmatrix}
x \\\
y
\end{pmatrix}
\mod N
$
**行列式分析**:变换矩阵的行列式为:
$
\det
\begin{pmatrix}
1 & 1 \\\
1 & 2
\end{pmatrix}
= 1 \times 2 - 1 \times 1 = 1
$[✅]渲染效果:
对于
的正方形图像,狭义Arnold变换的数学表达式为: 其矩阵形式可表示为:
行列式分析:变换矩阵的行列式为:
结语
思维的碰撞,往往诞生于一场积极的交流;智慧的火花,常在热烈的讨论中闪耀。如果您在这片文字的海洋里,找到了共鸣或产生了独特的见解,不妨在评论区留下您的声音。我珍视每一位读者的思考,期待与您一同构建一个充满活力的思想社区。
同时,为了不错过更多精彩内容和深度交流的机会,也欢迎大家加入我:
无论是评论区的畅所欲言,还是在各个平台上与我们并肩同行,都将是推动我不断前行的动力。ByteWyrm,因您的参与而更加精彩!
- Thanks for your appreciation. / 感谢您的赞赏

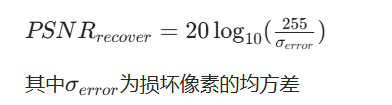





.jpg)
.jpg)
.jpg)




